Implication and Iff
The Symbols are 
and 
Implication:
Implication says "if ... then"
Example:
If both a and b are odd numbers then (a+b) is even
can be written as:
both a and b are odd numbers (a+b) is even
The reason it points to the right is that it might not be true the other way
Example:
Just because (a+b) is even does not mean that a and b are odd (they may both be even)
Iff: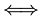
Iff says "if and only if"
It is an implication that goes both ways.
Example:
x + y = 3 x = 3 − y
That one is true both ways!
Example:
a and b are both integers.
If one of a and b is odd and the other is even then (a+b) is odd can be written as:
One of a and b is odd and the other is even (a+b) is odd
In this case it goes both ways, because if (a+b) is odd and a and b are both integers, then one of them must be odd and the other even.