Solving ASA Triangles

Example 1

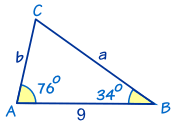
In this triangle we know:

• angle A = 76°
• angle B = 34°
• and c = 9

 

It's easy to find angle C by using 'angles of a triangle add to 180°':

So C = 180° − 76° − 34° = 70°

 

We can now find side a by using The Law of Sines:

a/sinA = c/sin C

a/sin76° = 9/sin70°

a = (9/sin70°) × sin76°
a = 9.29 to 2 decimal places

 

Similarly we can find side b by using The Law of Sines:

b/sinB = c/sin C

b/sin34° = 9/sin70°

b = (9/sin70°) × sin34°
b = 5.36 to 2 decimal places

 

Now we have completely solved the triangle i.e. we have found all its angles and sides.

Example 2

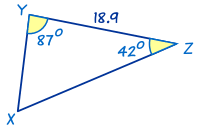
This is also an ASA triangle.

First find angle X by using 'angles of a triangle add to 180°':

X = 180° − 87° − 42° = 51°

Now find side y by using The Law of Sines:

y/sinY = x/sin X

y/sin(87°) = 18.9/sin(51°)

y = (18.9/sin(51°)) × sin(87°)
y = 24.29 to 2 decimal places.

Similarly we can find z by using The Law of Sines:

z/sinZ = x/sin X

z/sin(42°) = 18.9/sin(51°)

z = (18.9/sin(51°)) × sin(42°)
z = 16.27 to 2 decimal places.